Vertraust du deinen Berechnungen?
Diese Buchreview handelt von The Los Alamos Primer, the first lectures on how to build an atomic bomb, von Robert Serber. Die Review handelt von den grundlegenden Berechnungen und das physikalische Wissen der Wissenschaftler des Manhattan-Projekts. Da der Primer eine Sammlung von Vorlesungsnotizen aus dem Jahr 1943 ist, die Serber nachträglich kommentiert hat, werden einige der ursprünglichen Berechnungen und Messungen anhand moderner Werte korrigiert. Das macht es faszinierend zu sehen, wie richtig oder falsch die Physiker damals lagen. Allen, die sich für dieses Thema interessieren, empfehle ich, sowohl den Primer als auch The Making of the Atomic Bomb von Richard Rhodes (eines der besten Bücher die ich gelesen habe) zu lesen.
Die Geschichte hinter dem Primer ist bemerkenswert: Die Vorlesungen wurden im Frühjahr 1943 allen Physikern gegeben, die nach Los Alamos kamen. Es ist faszinierend, dieselben Notizen zu lesen, die jene Personen benutzten, die für den Bau der ersten Atombombe verantwortlich waren. Mein Hauptziel in dieser Review ist es, die wesentlichen physikalischen Konzepte einfach und verständlich zu halten, während ich gelegentlich tief in die Berechnungen eintauche, um das Wissen und auch die Unsicherheiten in den Zahlen der damaligen Wissenschaftler darzustellen.
Entwicklung einer praktikablen militärischen Waffe
Zunächst ist wichtig zu verstehen, dass das Manhattan-Projekt ein klares Ziel hatte: eine praktikable militärische Waffe von enormer Zerstörungskraft zu bauen. Auch wenn das extrem klingt, war die Hauptmotivation, Nazi-Deutschland zu übertreffen und den Gesamtschaden zu minimieren. Im Originaltext heißt es:
The object of the project is to produce a practical military weapon in the form of a bomb in which the energy is released by a fast neutron chain reaction in one or more of the materials known to show nuclear fission.
In den Vorlesungen wurde das Wort Bombe durch Gadget ersetzt, und mit „praktisch“ meinte man, dass die Bombe leicht und klein genug sein sollte, um von einem Flugzeug transportiert zu werden – nicht ein mehrere Tonnen wiegender Gegenstand wie ein Kernreaktor.
Der grundlegende Prozess, der beim Bau der ersten Kernwaffen ausgenutzt wurde, war die Freisetzung von Energie durch die Kernspaltung (später wurden Wasserstoffbomben auf der Basis der Kernfusion entwickelt). In den frühen 1930er-Jahren bombardierten Enrico Fermi und seine Kollegen verschiedene Atomkerne mit Neutronen in der Annahme, dass dadurch diese Elemente in andere Elemente mit höherer Massenzahl umwandeln würden. Erst im Winter 1938 analysierten Otto Hahn, Fritz Strassmann, Lise Meitner und Otto Frisch die Reaktionsprodukte der Neutronenbestrahlung von Uran und entdeckten, dass der Prozess zur Spaltung des Atmokerns führte und nicht zur Transmutation. Ihre bahnbrechende Erkenntnis zeigte, dass unter den natürlich vorkommenden Elementen nur Uran (insbesondere das spaltbare Isotop $\mathrm{U}^{235}_{92}$) durch Neutronen gespalten werden kann. Obwohl in frühen Kernwaffen letztlich sowohl Uran als auch künstlich erzeugtes Plutonium eingesetzt wurden, war es doch die Fähigkeit von Uran, sich durch Neutronen spalten zu lassen, welche die Grundlage für die Atombombe bildete.
Überschlagsmäßige Energiebetrachtungen
Um einige alltägliche Energievergleiche zu ermöglichen, folgt hier eine Tabelle mit Energieeinheiten (alle haben dieselbe Dimension $\frac{M L^2}{T^2}$):
| J (Joule) | kWh | cal (Kalorie) | eV (Elektronenvolt) | erg | kt (Kilotonnen) TNT |
|---|---|---|---|---|---|
| $1 \text{ J}$ | $3.6 \times 10^6 \text{ J}$ | $4.184 \text{ J}$ | $1.602 \times 10^{-19} \text{ J}$ | $10^{-7} \text{ J}$ | $4.184 \times 10^{12} \text{ J}$ |
Bei der Spaltung eines schweren Kerns wie Uran wird eine enorme Energiemenge frei. Bei einem typischen Spaltungsereignis werden etwa $$ 200 \text{ MeV} \approx 3,2 \times 10^{-11} \text{ J} $$ freigesetzt. Im Gegensatz dazu liegt die bei einer chemischen Reaktion (z. B. Verbrennung) freiwerdende Energie pro Bindung typischerweise in der Größenordnung von $$ 1 \text{ eV} \approx 1,6 \times 10^{-19} \text{ J}, $$ was bedeutet, dass Kernspaltung pro Ereignis etwa $10^8$-mal energiereicher ist als chemische Prozesse. Da bei einer Detonation die freigesetzte Energiemenge entscheidend ist, wurde den Physikern schnell klar, dass eine auf Spaltung basierende Waffe eine enorme Zerstörungskraft besitzen würde.
Die Energie, die bei der Spaltung eines Uran-Kerns frei wird, lässt sich durch Bindungsenergieberechnungen verstehen, in denen die elektrostatische (Coulomb-)Abstoßung zwischen den Protonen berücksichtigt wird. Zwar wird die Energiedifferenz oft über Einsteins Masse-Energie-Äquivalenz $E = mc^2$ ausgedrückt, doch dient diese Beziehung lediglich dazu, die Differenz in der Bindungsenergie als äquivalente Massendifferenz darzustellen. Sie bedeutet nicht, dass relativistische Effekte bei der Spaltung selbst eine Rolle spielen.
Betrachten wir einen $\mathrm{U}^{238}$-Kern mit $Z=92$, $N=146$ und $A=238$. Die Energie aus den wirkenden Coulombkräften kann mit folgender Formel abgeschätzt werden: $$ E = \frac{1}{4\pi\epsilon_0}\frac{3}{5}\frac{Q^2}{R} \quad \text{mit} \quad Q = Z e. $$ Setzt man $$ \frac{e^2}{4\pi\epsilon_0} \approx 1,44 \text{ MeV}\cdot\text{fm} \quad \text{und} \quad R \approx 7,4 \text{ fm}, $$ erhält man $$ E_{\text{U}} \approx \frac{3}{5}\frac{1,44 \times (92)^2}{7,4}\text{ MeV}. $$
Da $92^2 \approx 100^2 = 10^4$, $1,44 \approx 1,5$ und $7,4 \approx 8$, folgt $$ E_{\text{U}} \approx \frac{3}{5}\frac{1,4 \times 10^4}{8} \text{ MeV} \approx 1050 \text{ MeV}. $$
Nimmt man eine symmetrische Spaltung in zwei Fragmente mit jeweils $Z\approx46$ und $A\approx119$ an, sinkt der Radius der Fragmente um den Faktor $\frac{1}{\sqrt[3]{2}}$, was ergibt: $$ R_{\text{frag}} \approx 7,4 \times \frac{1}{\sqrt[3]{2}} \approx 5,9 \text{ fm}. $$
Die Coulomb-Energie eines Fragments (angenommen $46 \approx 50$) ist dann $$ E_{\text{frag}} \approx \frac{3}{5}\frac{1,4 \times 50^2}{6} \approx 350 \text{ MeV}. $$
Die Änderung der Coulomb-Energie durch Spaltung beträgt somit $$ \Delta E \approx E_{\text{U}} - 2 \times E_{\text{frag}} \approx 1050 - 700 \approx 350 \text{ MeV}, $$ wobei tatsächlich etwa $\Delta E \approx 350 \text{ MeV}$ pro Spaltungsereignis freiwerden, weil die Coulomb-Energie des ursprünglichen Kerns durch die Aufspaltung in zwei kleinere Fragmente verringert wird.
Energiefreisetzung bei teilweiser Spaltung
In praktischen Anwendungen (sowohl in Bomben als auch in Reaktoren) ist es sehr schwierig, eine vollständige Spaltung des gesamten spaltbaren Materials zu erreichen. Nehmen wir beispielsweise an, nur 1% des Urans in einer Probe würde gespalten. Betrachten wir 1 g Uran-235. Die Anzahl der Atome in 1 g beträgt $$ N \approx \frac{N_A}{235} \approx \frac{6,022 \times 10^{23}}{235} \approx 2,5 \times 10^{21} \text{ Atome}. $$ Wenn nur 1% davon gespalten wird, ist die Anzahl der Spaltungen $$ N_{\text{fission}} \approx 0,01 \times 2,5 \times 10^{21} \approx 2,5 \times 10^{19}. $$ Da jede Spaltung etwa $5 \times 10^{-11} \text{ J}$ freisetzt, ergibt sich eine gesamte freigesetzte Energie von $$ E_{\text{total}} \approx 2,5 \times 10^{19} \times 5 \times 10^{-11} \text{ J} \approx 12 \times 10^{8} \text{ J}. $$ Umgerechnet in Kilowattstunden: $$ \frac{12 \times 10^{8} \text{ J}}{3,6 \times 10^{6} \text{ J}/\text{kWh}} \approx 300 \text{ kWh}. $$
Vergleicht man das mit dem Fall, dass $100$ % des 1 g Uran gespalten würden, so ließe sich eine Energiemenge von etwa $30000 \text{ kWh}$ freisetzen – das ist etwa das Zehnfache des durchschnittlichen Jahresverbrauchs eines österreichischen Haushalts (rund $3500 \text{ kWh}$ pro Jahr). Dieser Unterschied verdeutlicht die enorme Energiedichte von Kernbrennstoffen: Selbst eine winzige Masse könnte im Prinzip eine Energiemenge liefern, die dem Jahresbedarf eines ganzen Haushalts entspricht, sofern eine vollständige Spaltung möglich wäre.
Frühe Kernwaffen: Ein kurzer Vergleich
Nachfolgend eine Tabelle zu den ersten drei Atombomben beim Trinity-Test und jene abgeworfene über Hiroshima und Nagasaki. Zwar variieren die genauen Zahlen je nach Quelle, doch verdeutlichen sie die relative Masse an spaltbarem Material, den Wirkungsgrad (den Anteil, der tatsächlich gespalten wurde) und den Unterschied zwischen maximaler theoretischer Sprengkraft (falls das gesamte Material gespalten werden würde) und der tatsächlich erzielten Sprengkraft.
| Gerät | Material | Masse (kg) | Wirkungsgrad (%) | Theoretische Sprengkraft (kt TNT) | Tatsächliche Sprengkraft (kt TNT) |
|---|---|---|---|---|---|
| Trinity | Pu-239 | ~6.2 | ~17 | ~105 | ~21 |
| Little Boy | U-235 | ~64 | ~1.5 | ~1000 | ~15 |
| Fat Man | Pu-239 | ~6.2 | ~17 | ~105 | ~21 |
Diese Schätzungen verdeutlichen sowohl das gewaltige Energiepotenzial der Kernspaltung als auch die technischen Herausforderungen, einen hohen Wirkungsgrad in der Praxis zu erreichen.
Kettenreaktion
Die Spaltung des Atoms ist nur die halbe Erklärung dafür, warum das Beschießen eines Atomkerns mit Neutronen so viel Energie freisetzen kann. Wenn ein Atomkern durch ein Neutron gespalten wird, entstehen nicht nur zwei oder mehr Fragmente, sondern es werden auch zusätzliche Neutronen emittiert, die weitere Atomkerne treffen können. Die zentrale Frage lautet: Wie viele Neutronen werden im Durchschnitt bei jedem Spaltungsereignis frei? Nur wenn diese durchschnittliche Zahl mindestens 1 beträgt, kann sich der Prozess selbst erhalten oder sogar beschleunigen, was zu einer Kettenreaktion führt. Mit „Kettenreaktion“ ist das exponentielle Wachstum der Anzahl an gespaltenen Atome gemeint. Wenn beispielsweise zwei Neutronen pro Spaltung freiwerden, verläuft die Sequenz 1, 2, 4, 8, 16, … und so weiter, beschreibbar durch
$$ N(t) = N_0 \times k_{eff}^t, $$
wobei $N(t)$ die Anzahl der zum Zeitpunkt $t$ gespaltenen Atome ist und $k_{eff}$ der effektive Fortpflanzungsfaktor. Er muss größer als 1 sein, eher in der Größe von etwa 2, damit in einer Atombombe in kurzer Zeit sehr viel Energie freigesetzt werden kann.
Da die durchschnittliche Neutronenzahl pro Spaltung (kurz Neutronenzahl) ist im Spaltungsprozess wichtig und wird üblicherweise mit $\nu$ bezeichnet. Dieser Wert hängt stark von der Energie der einfallenden Neutronen und vom Material selbst ab. Eine weitere wichtige Materialeigenschaft ist der Spaltungsquerschnitt. Jeder Atomkern besitzt einen geometrischen Querschnitt $\sigma$, der seine Größe widerspiegelt. Der Anteil der Zusammenstöße, die tatsächlich eine Spaltung hervorrufen, multipliziert mit $\sigma$ ergibt den Spaltungsquerschnitt $\sigma_f$. Wenn ein Neutron keine Spaltung hervorruft, kann es erneut emittiert werden, entweder mit geringerer Energie (inelastische Streuung) oder nahezu gleicher Energie (elastische Streuung). Letzteres ist ein quantenmechanischer Prozess. Bei sehr niedrigen Neutronenenergien können Quanteneffekte (aus der Heisenbergschen Unschärferelation) so stark sein, dass der Spaltungsquerschnitt größer ist als der geometrische Querschnitt. Wir werden in den kommenden Abschnitten sehen, dass diese langsamen Neutronen (wenig kinetische Energie) in den Prozessen einer Atombombe nicht ausgenutzt werden können.
Elemente
Neben der Neutronenzahl $\nu$ und dem Spaltungsquerschnitt $\sigma_f$ ist es für ein Material auch interessant, welche Energie ein einfallendes Neutron haben muss, um eine Spaltung auszulösen, und wie viel Energie die bei einem Spaltungsprozess emittierten Neutronen besitzen.
Das einzige natürlich vorkommende Element, das zum Bau der ersten Atombomben verwendet wurde, war Uran in der Form $\text{U}^{238}$. Nur ein 140stel davon ist $\text{U}^{235}$, das weitaus leichter spaltbare Isotop. Das dritte verwendete Element für den Bau der ersten Atombomben war $\text{Pu}^{239}$, das nur künstlich als Nebenprodukt einer langsamen nuklearen Kettenreaktion erzeugt werden kann. Wie in den folgenden Diagrammen und der Tabelle zu sehen ist, haben diese beiden letztgenannten Elemente deutlich bessere Spaltungseigenschaften als das natürlich vorkommende $\text{U}^{238}$. Daraus ergab sich die größte Herausforderung beim Bau der ersten Atombombe: eine Industrie zu errichten, um $\text{U}^{235}$ anzureichern (wie in Oak Ridge durch Diffusions- und elektromagnetische Trennverfahren) oder $\text{Pu}^{239}$ in Kernreaktoren zu synthetisieren (wie in Hanford). Beide Prozesse waren sehr schwierig zu entwickeln und erforderten enorme finanzielle und personelle Ressourcen. Oft wird übersehen, dass nur die Vereinigten Staaten wirtschaftlich in der Lage waren, diese Industrie von Grund auf aufzubauen. Alle anderen Länder hatten Kriegsschauplätze in ihrem Land und somit war es deutlich schwieriger eine neue Industrie zu errichten.
Nun betrachten wir zwei wichtige Diagramme. Das erste zeigt die Energie einfallender Neutronen in Abhängigkeit vom Spaltungsquerschnitt für die drei betrachteten Materialien. Man sieht, dass $\text{U}^{235}$ und $\text{Pu}^{239}$ deutlich spaltbarer sind als das natürlich vorkommende $\text{U}^{238}$. Die zweite Grafik zeigt die Energieverteilung der bei einem Spaltungsprozess emittierten Neutronen. Diese Verteilungen sind bei den drei Materialien nahezu gleich.
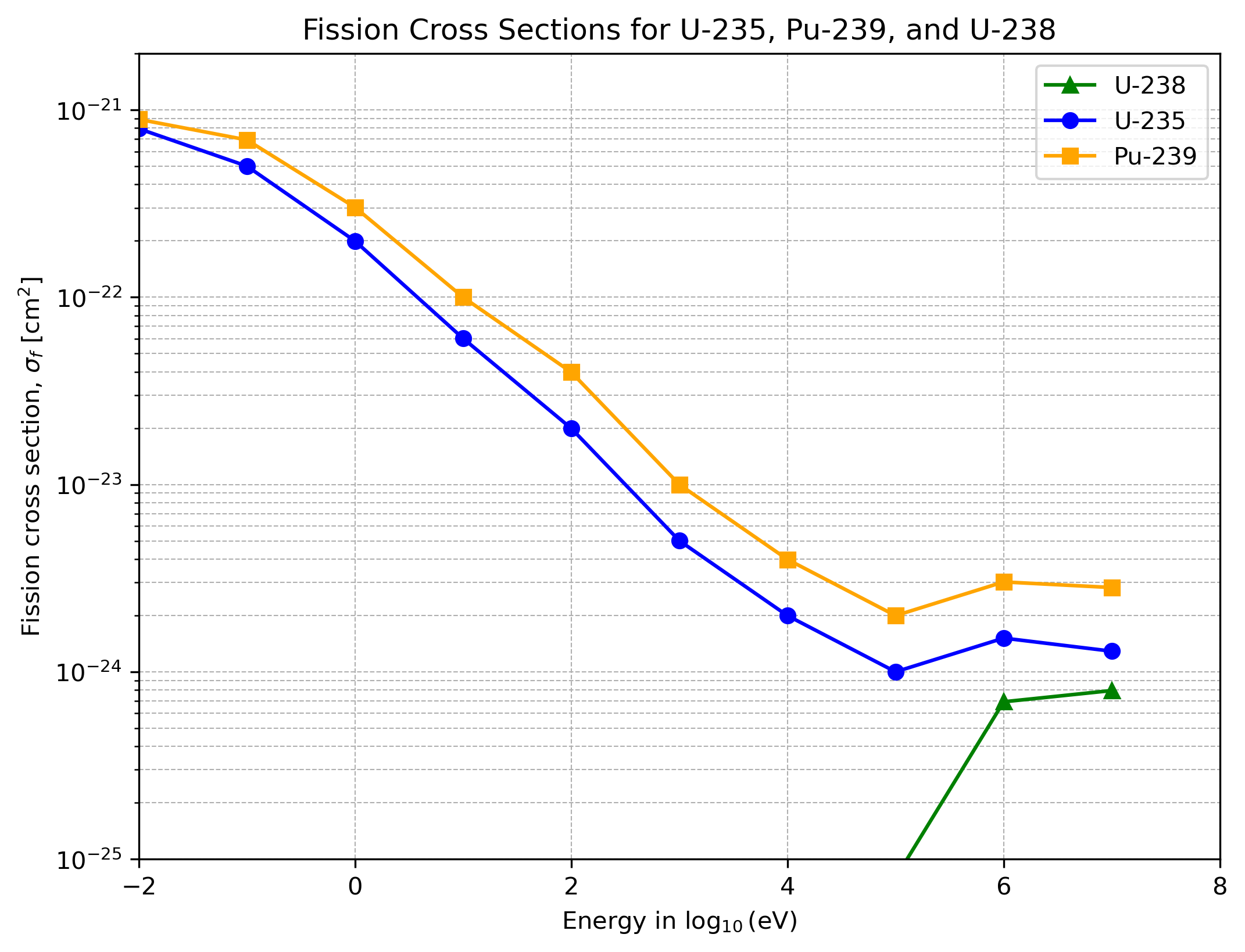
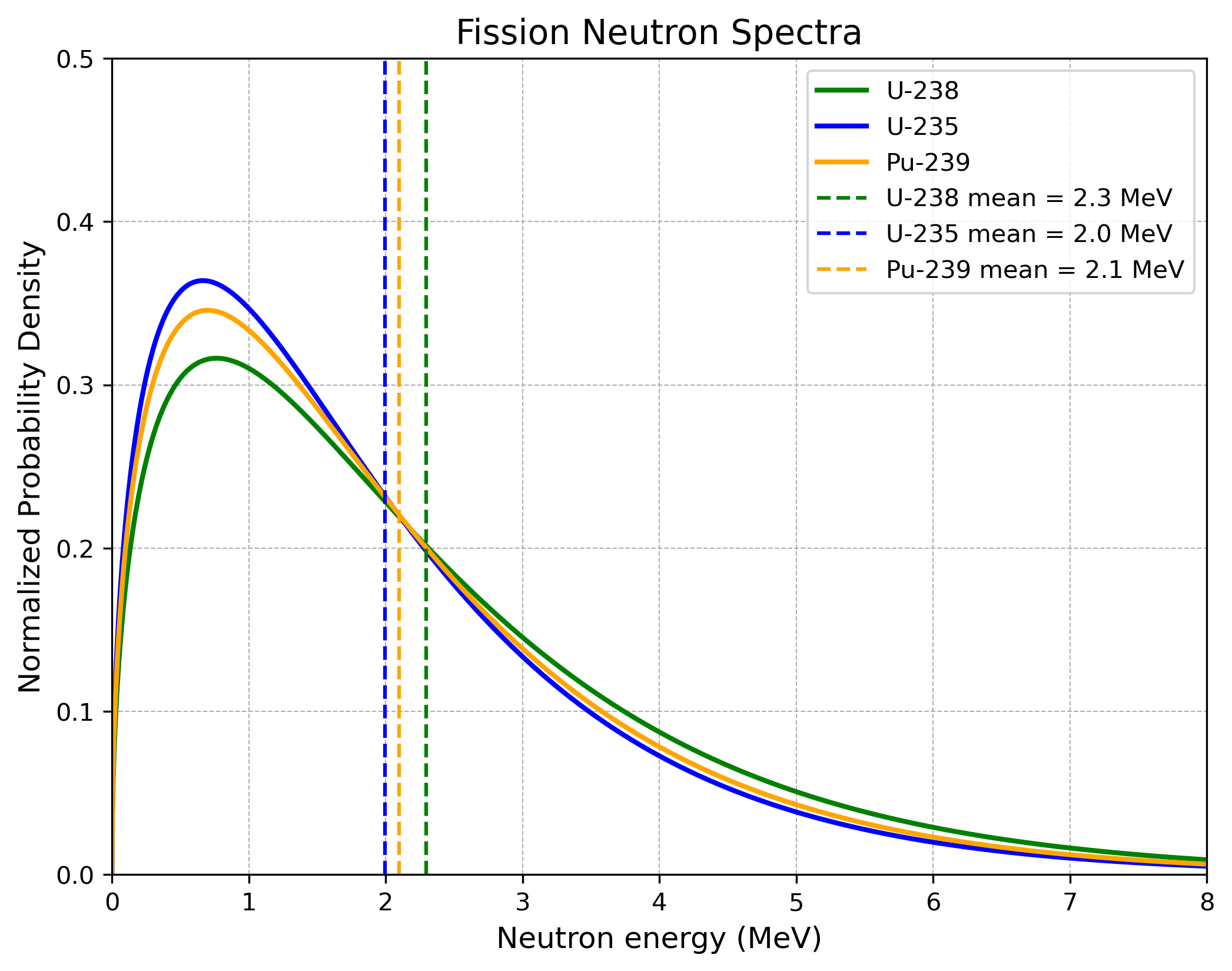
Die Kernaussage dieser beiden Diagramme würde nahelegen, dass man langsame Neutronen nutzen sollte, um hohe Spaltungsquerschnitte auszunutzen und alle langsam emittierten Neutronen aus den Spaltungen zu verwenden. Obwohl diese Tatsachen in Kernreaktoren genutzt werden, ist das in einer Atombombe nicht möglich. Warum das so ist, wird im nächsten Abschnitt erläutert.
Wie sieht es mit den Neutronenzahlen aus? In der folgenden Tabelle sind die Schätzungen von damals und die heutigen Messwerte für Neutronenzahlen und Spaltungsquerschnitte aufgeführt (diese Werte beziehen sich auf energiereiche einfallende Neutronen aus obigem Diagramm). Außerdem ist die Größe $(\nu - 1) \times \sigma_f$ dargestellt, da Neutronenzahl und Spaltungsquerschnitt in den kommenden Betrachtungen zur kritischen Masse stets zusammen auftreten. Bemerkenswert ist, dass die Schätzungen der Einzelwerte zum Teil deutlich abwichen aber die kombinierte Zahl sehr nahe am tatsächlichen Wert. (Die Spaltungsquerschnitte sind in $10^{-24} \text{ cm}^2$ angegeben.)
| Isotop |
$\sigma_f$ (frühe Schätzung) |
$\sigma_f$ (aktuell) |
$\nu$ (frühe Schätzung) |
$\nu$ (aktuell) |
$(\nu-1) \, \sigma_f$ (frühe Schätzung) |
$(\nu-1) \, \sigma_f$ (aktuell) |
|---|---|---|---|---|---|---|
| U‑235 | 1.5 | 1.22 | 2.20 | 2.52 | 1.80 | 1.85 |
| Pu‑239 | 3.0 | 1.73 | 2.20 | 2.95 | 3.60 | 3.40 |
Langsame vs. schnelle Spaltung
Nun kommen wir zur Frage, die sich aus den letzten Beiden Abschnitten ergibt: warum langsame Neutronenspaltung nicht verwendet werden kann? Es wäre tatsächlich sehr attraktiv, die höheren Spaltungsquerschnitte zu nutzen, die sich durch Quanteneffekte bei langsamen Neutronen ergeben (wie in den obigen Diagrammen für $\text{U}^{235}$ und $\text{Pu}^{239}$ zu sehen ist). In Kernreaktoren wird diese langsame Neutronenspaltung tatsächlich genutzt. Der entscheidende Unterschied zwischen einer Bombe und einem Reaktor liegt jedoch im effektiven Neutronenvermehrungsfaktor: In einem Reaktor wird dieser Wert auf etwa 1 geregelt, während er in einer Atombombe bei 2 oder sogar höher liegt. Um den Vermehrungsfaktor nahe 1 zu halten, müssen die emittierten Neutronen in Moderatormaterialien aufgenommen und abgebremst werden (hauptsächlich durch elastische Streuung). Die niedrige Vermehrungszahl stellt außerdem sicher, dass die freigesetzte Energie kontrollierbar bleibt und der Reaktor nicht überhitzt.
Ist dieser Faktor hingegen hoch, wird in kleinem Volumen eine gewaltige Energiemenge frei, sodass sich das Material sehr schnell ausdehnt. Eine kurze Rechnung zeigt warum. Angenommen, 1% der Energie aus der Spaltung eines Uranatoms (Masse $m=3,88 \times 10^{-25} \text{ kg}$) wird in Expansionsgeschwindigkeit umgewandelt (mit $E=\frac{1}{2} m v^2$), und jedes Atom setzt $E = 350 \text{ MeV} \approx 5 \times 10^{-11} \text{J }$ frei, dann gilt:
$$ 0,01 \times 5 \times 10^{-11} = 3,88 \times 10^{-25} \times v^2 \Longrightarrow v \approx 1,1 \times 10^6 \tfrac{\text{m}}{\text{s}}. $$
Bei solchen Geschwindigkeiten fällt die Dichte des Bombenmaterials rasch ab, und das System wird in etwa $10^{-8} \text{s}$ unterkritisch, sodass die Kettenreaktion stoppt. Daher kann eine Atombombe trotz höherer Spaltungsquerschnitte nicht auf langsamer Neutronenspaltung beruhen – es fehlt einfach die Zeit und ein Mechanismus, um Neutronen zu moderieren und abzubremsen, und das sich schnell ausdehnende Bombenmaterial führt dazu, dass schnelle Spaltung der dominierende Prozess bleibt.
Kritische Masse
Um eine brauchbare Abschätzung für die kritische Masse einer bestimmten Geometrie und eines bestimmten Materials zu erhalten, verwendeten die Wissenschaftler in Los Alamos zunächst die gewöhnliche Diffusionstheorie. Obwohl die einfache Diffusionstheorie aus der Statistischen Mechanik nicht exakt anwendbar ist (weil die mittlere freie Weglänge der Neutronen oft größer ist als die Ausmaße des Systems), reicht sie für eine grobe Schätzung der kritischen Masse aus. Wir haben zuvor angenommen, dass die Zeit zwischen Spaltungsereignissen in der Größenordnung $ \tau \approx 10^{-8} \text{ s}$ liegt und die durchschnittliche Zahl von Neutronen pro Spaltung, $\nu$, zwischen 2 und 3. Bezeichne $N(t)$ als die Anzahl der Neutronen zum Zeitpunkt $t$. Dann gibt die Diffusionstheorie folgenden Ansatz: $$ \dot{N} + \nabla \cdot \mathbf{j} = \frac{\nu - 1}{\tau} N $$ vor, wobei $\dot{N}$ die Zeitableitung von $N$ ist und $\mathbf{j}$ der Diffusionsstrom der Neutronen durch die Materialgrenze (abhängig von der Geometrie). In der einfachen Diffusionstheorie nimmt man an: $$ \mathbf{j} = -D \nabla N, $$ wobei $D$ die Diffusionskonstante ist, die von der Neutronengeschwindigkeit (wie oben berechnet) und den Wirkungsquerschnitten des Materials abhängt. Durch Einsetzen dieser Beziehung in die obige partielle Differenzialgleichung vereinfacht sich diese zu $$ \dot{N} = D \nabla^2 N + \frac{\nu - 1}{\tau} N. $$ Wichtig ist, dass $\dot{N}$ eine Zeitableitung darstellt, während der Laplace-Operator $\nabla^2$ (aus der Divergenz des Gradienten) räumliche Ableitungen enthält.
In dieser partiellen Differenzialgleichung kann man den räumlichen und den zeitabhängigen Teil von $N$ trennen: $$N(t, x, y, z) = N_1(x, y, z) \exp\left(\frac{\nu’ t}{\tau}\right), $$ wobei $\nu’$ die effektive Neutronenzahl ist – also der Anteil der pro Spaltung freiwerdenden Neutronen, der tatsächlich weitere Spaltungen hervorruft. (Häufig definiert man $ \nu’ = (\nu - 1) \frac{ \sigma_f}{\sigma_t}$, damit nur die „überschüssigen“ Neutronen gezählt werden, die weitere Spaltungen auslösen.) Um den Punkt zu finden, an dem die Masse kritisch wird, sucht man nach einer räumlichen Funktion $N_1(x,y,z)$, die $$ \nabla^2 N_1 + \frac{-\nu’ + \nu - 1}{D \tau} N_1 = 0 $$ erfüllt. Diese Differenzialgleichung muss für die gewünschte Geometrie und passende Randbedingungen gelöst werden. Ich rechne im Folgenden sowohl für eine Kugel als auch für einen Würfel, um den Einfluss der Geometrie zu zeigen. Danach verwende ich den Kugelfall weiter, weil die Bomben ebenfalls kugelförmig waren. Die Randbedingungen werden vereinfacht, indem wir $N=0$ am Kugelradius bzw. an den Kanten des Würfels mit Kantenlänge $a$ annehmen.
Für die Kugel und Kugelkoordinaten ergibt sich die Lösung: $$ N_1(r)=\frac{\sin\Bigl(\frac{\pi r}{R}\Bigr)}{r}, $$ was nach Einsetzen und Vereinfachen in der obigen Differenzialgleichung zu $\nu’ = (\nu - 1) + \frac{\pi^2 D \tau}{R^2}$ führt. Setzt man dies gleich Null und löst nach $R$ auf, erhält man den kritischen Radius: $$ R_{\rm crit}=\pi\sqrt{\frac{D\tau}{\nu-1}}. $$
Nimmt man als Beispiel für $\text{U}^{235}$ eine durchschnittliche Neutronenzahl von $\nu\approx2,5$ (also $\nu-1\approx1,5$) und nimmt an, dass bei schnellen Neutronen $D\tau \approx 13,7 \text{ cm}^2$ gilt, findet man: $$ R_{\rm crit}\approx \pi\sqrt{\frac{13,7}{1,5}} \approx 9,5 \text{ cm} \Longrightarrow M_{\rm crit}\approx 68 \text{ kg}, $$ wenn man eine Dichte $\rho\approx 19 \text{ g/cm}^3$ und die Volumenformel für eine Kugel verwendet.
Die Lösunge für den Würfel hat folgende Form: $$ N_1(x,y,z)=\sin\Bigl(\frac{\pi x}{a}\Bigr)\sin\Bigl(\frac{\pi y}{a}\Bigr)\sin\Bigl(\frac{\pi z}{a}\Bigr), $$ was nach wiederholtem Einsetzen und Auflösen zu $\nu’ = (\nu - 1) + \frac{3\pi^2 D \tau}{a^2}$ führt. Daraus löst man für die kritische Kantenlänge $a_{\rm crit}$: $$ a_{\rm crit}=\pi\sqrt{\frac{3D\tau}{\nu-1}}. $$ Man kann sehen, dass $a_{\rm crit}=\sqrt{3}R_{\rm crit}$. Setzt man dieselben Zahlenwerte ein, folgt $$ a_{\rm crit}\approx\sqrt{3}\times 9,5 \text{ cm}\approx 16,5 \text{ cm} \Longrightarrow M_{\rm crit}^{\rm (cube)}\approx(16,5 \text{ cm})^3\times 19 \text{ g/cm}^3\approx 85 \text{ kg}.$$
Man kann zeigen, dass aufgrund der ungünstigeren Geometrie die kritische Masse beim Würfel um den Faktor $$ \frac{M_{\rm cube}}{M_{\rm sphere}}\approx\frac{3^{5/2}}{4\pi}\approx1,24 $$ größer ist.
Dies sind stark vereinfachte Berechnungen. Tatsächlich liegt der kritische Radius und die kritische Masse für eine nicht umhüllte Kugel aus $\text{U}^{235}$ etwa bei $$ R_{\rm crit}\approx10 \text{ cm}\quad \text{und}\quad M_{\rm crit}\approx60\text{–}70 \text{ kg}. $$ Eine detailliertere Analyse der Diffusionskonstante $D$ und der Neutronengenerationszeit $\tau$ ergibt schließlich, dass die kritische Masse von den Materialeigenschaften ungefähr wie folgt abhängt: $$ M_{\rm crit}\propto \frac{1}{\rho^2}\frac{1}{\bigl[\sigma(\nu-1)\bigr]^{3/2}}. $$
Wirkungsgrad
Ein zweiter wichtiger Faktor im Manhattan-Projekt war, den Wirkungsgrad der Bombe zu maximieren. Mit „Wirkungsgrad“ ist hier das Verhältnis zwischen der tatsächlich bei der Spaltung freiwerdenden Energie und dem theoretischen Maximum gemeint, wenn das gesamte spaltbare Material gespalten werden würde. Unsere früheren Schätzungen lagen in der Größenordnung von 1%. Jetzt müssen wir klären, woher dieser Wert kommt. Der Hauptgrund ist, dass die Kettenreaktion abbricht, sobald die Bombe sich rasch ausdehnt und die Dichte unter den kritischen Wert fällt. Außerdem wird sich zeigen, dass größere Bomben, die ein Vielfaches der kritischen Masse haben, einen höheren Wirkungsgrad aufweisen.
Sei $R_{cn}$ der kritische Radius bei normaler Dichte $\rho_n$ und $R_n$ der anfängliche (superkritische) Radius der Bombe. Da die Masse $M \propto R^3$ skaliert, gilt für das Beispiel, wo eine Bombe die doppelte kritische Masse besitzt (also $M_n/M_{cn} = 2$): $$ \left(\frac{R_n}{R_{cn}}\right)^3 = 2, $$ folglich $$ R_n = \sqrt[3]{2} R_{cn} \approx 1,26 R_{cn} . $$ Wir definieren den überschüssigen Radius mit Delta $$ \delta = \frac{R_n - R_{cn}}{R_{cn}}, $$ sodass in diesem Beispiel $\delta \approx 0,26$ gilt.
Eine zentrale Annahme ist, dass die Kettenreaktion bei Radius $R$ aufhört, wenn sich die Kugel um etwa die Hälfte dieses Überschusses ausgedehnt hat: $$ R - R_n = \frac{1}{2} \delta R_{cn} . $$ Diese Annahme ist nicht streng hergeleitet, sondern dient als praktisches Kriterium dafür, wann die Dichte so weit gesunken ist, dass keine anhaltende Spaltung mehr möglich ist.
Als Nächstes betrachten wir eine einfache Energiebilanz. Wir nehmen an, dass die Ausbreitungsgeschwindigkeit nach außen durch $$ v \approx \frac{\nu’}{\tau}(R - R_n) $$ gegeben ist, wobei $\tau \approx 10^{-8} \text{ s}$ die Neutronengenerationszeit darstellt und $\nu’$ der effektive Neutronenmultiplikator ist. Der Faktor $\frac{\nu’}{\tau}$ gibt die Zeitskala des exponentiellen Wachstums der Neutronenzahl an. In unserem Modell wird angenommen, dass pro Gramm spaltbarem Material (z. B. $\text{U}^{235}$) etwa $E \approx 12 \times 10^{13} \text{ J/kg}$ an Energie freigesetzt wird.
Wir nehmen an, dass ein Anteil $f$ dieser Spaltungsenergie $E$ (in J/kg) in kinetische Energie der Expansion umgewandelt wird. Nur diese Energie wird frei, bevor die Spaltungsprozesse aufhören. Die kinetische Energie pro Kilogramm ist $$ \frac{1}{2}v^2, $$ wobei die Ausdehnungsgeschwindigkeit $v \approx \frac{\nu’}{\tau}(R - R_n)$ ist. Hier ist $\tau \approx 10^{-8} \text{ s}$ der Zeitabstand zweier Spaltungen, und $\nu’ \approx \nu - 1 \approx 1,5$ die effektive Neutronenzahl. Wir nehmen außerdem an, dass die Kettenreaktion endet, wenn sich die Bombe um eben jenen Überschuss $\frac{1}{2} \delta R_{cn} $ ausgedehnt hat.
Dann wird die Ausbreitungsgeschwindigkeit $$ v \approx \frac{\nu - 1}{\tau}\left(\frac{1}{2} \delta R_{cn} \right). $$ Daraus folgt für die kinetische Energie pro Kilogramm: $$ \frac{1}{2}v^2 \approx \frac{1}{2}\left[\frac{(\nu - 1) \delta R_{cn} }{2 \tau}\right]^2 = \frac{(\nu - 1)^2 \delta ^2 R_{cn} ^2}{8 \tau^2 }. $$
Setzt man nun voraus, dass diese kinetische Energie dem Bruchteil $f$ der verfügbaren Spaltungsenergie $E$ entspricht, so gilt: $$ f \times E = \frac{(\nu - 1)^2 \delta ^2 R_{cn} ^2}{8 \tau^2 }, $$ und damit folgt $$ f = \frac{(\nu - 1)^2 R_{cn} ^2}{8E \tau^2 } \delta ^2. $$
Wenn wir all diese Werte einsetzen und $R_{cn} \approx 0,09 \text{ m}$ verwenden, erhalten wir folgendes Ergebnis: $$f \approx \frac{0.00123}{0.096} \approx 0.0128,$$ also etwa 1,3%. Unter Berücksichtigung von Ungenauigkeiten und Vereinfachungen ist das eine Größenordnung von rund 1% Wirkungsgrad.
Daher erreicht eine Bombe mit doppelter kritischer Masse trotz des deutlichen Anfangsübergewichts nur einen Wirkungsgrad von etwa 1%, weil die schnelle hydrodynamische Expansion die Zahl der möglichen Spaltungsgenerationen stark begrenzt. Wir sehen also, dass der Wirkungsgrad ein wichtiges Thema und ein möglicher Verbesserungsbereich ist. Heutige Werte liegen übrigens bei etwa 1–5 %.
Tamper
Unter dem Begriff Tamper versteht man eine zusätzliche Schicht Material, die um den angereicherten Kern gelegt wird. Diese erfüllt zwei Hauptaufgaben:
-
Neutronenreflexion: Der Tamper reflektiert Neutronen, die sonst durch die Grenze entweichen würden, wieder zurück ins Material. Dadurch verbessern sich die Randbedingungen der Diffusionsgleichung, was die benötigte kritische Masse für eine Kettenreaktion senkt. Beispielsweise kann eine Tamper-Schicht von 2–3 cm Dicke aus einem dichten Material wie Gold oder $\text{U}^{238}$ die kritische Masse im Vergleich zu einem System ohne Tamper um ungefähr den Faktor 4 verringern.
-
Trägheitsverzögerung: Der Tamper erhöht die Masse der Bombe und somit auch ihre Trägheit. Diese zusätzliche Masse verlangsamt die Expansion des Kerns während der Explosion. Obwohl das der Kettenreaktion etwas mehr Zeit gibt, ist die Auswirkung auf den Wirkungsgrad insgesamt begrenzt. Laut Erklärung im Primer bleibt der Wirkungsgrad selbst mit Tamper recht niedrig (nicht viel höher als die erwähnten 1–2 %), weil die für die Kettenreaktion verfügbare Zeit extrem kurz ist (im Bereich von $\tau \sim 10^{-8} \text{ s}$).
Zusammengefasst kann der Tamper die kritische Masse durch bessere Neutronenreflexion deutlich reduzieren, während sein Effekt auf den Wirkungsgrad der Explosion vergleichsweise gering bleibt.
Bombendesign
Der erste grundlegende Ansatz, tatsächlich eine Bombe zu konstruieren, die eine kritische Masse erreicht und eine große Energiemenge freisetzt, war der Kanonentyp (gun-type design). Die Idee bestand darin, zwei unterkritische Teile des Materials mithilfe konventioneller Sprengstoffe aufeinander zu schießen, sodass sie sich zu einer kritischen Masse vereinen. Die über Hiroshima abgeworfene Bombe Little Boy (mit $\text{U}^{235}$) basierte auf diesem Prinzip. Tatsächlich bewegte sich das Projektil mit etwa $300 \text{ m/s}$, und selbst bei dieser relativ hohen Geschwindigkeit „verpuffte“ ein großer Teil des Spaltstoffs vorzeitig, was zu einer geringen Effizienz führte (wie in der vorigen Tabelle zu sehen).
Der zweite, wesentlich anspruchsvollere und dennoch geniale Ansatz war der Implosionstyp (implosion-type design). Der Trinity-Test und die über Nagasaki abgeworfene Bombe Fat Man funktionierten nach diesem Prinzip. Da die kritische Masse von der Dichte abhängt (siehe „Kritische Masse“), wurde gewöhnlicher Sprengstoff um eine unterkritische Kugel aus $\text{Pu}^{239}$ gezündet, um sie zu komprimieren, ihre Dichte zu erhöhen und sie dadurch überkritisch zu machen. Zusätzlich dienten diese Sprengstoffe als Tamper, um die Bombe zusammenzuhalten und die kritische Masse weiter zu verringern. Dieses Design war eine enorme ingenieurtechnische und physikalische Herausforderung, weil man Stoßwellen in verschiedenen Materialien berechnen und die Effektivität der Sprengstoffe einschätzen musste. Ohne moderne Computer dauerten diese Strömungs- und Stoßwellenberechnungen sehr lange, und es blieb lange Zeit unsicher, ob dieses Konzept überhaupt gelingen würde.
Wohin führte das alles?
In diesem letzten Abschnitt geht es vor allem um die Zerstörungskraft und das Leid, das durch die Bomben verursacht wurde, die in den zwei Jahren nach diesen grundlegenden Berechnungen entwickelt wurden. Jeder muss für sich entscheiden, ob es richtig war, diese Bomben abzuwerfen – was für eine geringere Anzahl an Menschen großes Leid bedeutete –, um einen länger andauernden Krieg mit möglicherweise Millionen von Toten zu vermeiden. Es war zweifellos eine schwierige Entscheidung.
Gewiss erfordert der Bau einer Atombombe oder eines Reaktors weitreichende ingenieurtechnische Leistungen und eine komplette Industrie, um die Rohstoffe bereitzustellen. Dennoch ist es aufschlussreich zu sehen, dass mit relativ einfachen Annahmen und klassischer (newtonscher) Physik die Wissenschaftler die wesentlichen Prinzipien ableiteten, die das Projekt leiteten. Darüber hinaus zeigt der Primer, unter welchen grundlegenden Annahmen die Forscher damals arbeiteten.
Die Zerstörung, die durch die ersten Atombomben verursacht wurde, die am 6. und 9. August 1945 auf Hiroshima bzw. Nagasaki abgeworfen wurden, hatte viele Facetten. Die offensichtlichste, wenn auch nicht notwendigerweise gefährlichste, ist die Radioaktivität. Hinzu kommt die gewaltige Explosion durch die freiwerdende Energie. Diese Energie wirkt in zweifacher Weise: Erstens erzeugt sie eine Druckwelle, die Gebäude und Menschen im bestimmten Radius vernichtet. Zweitens entsteht ein großer Feuerball, der durch seine enorme Hitze nicht nur Gebäude und die Umgebung niederbrennt, sondern wahrscheinlich auch einen Feuersturm auslöst, der durch Wind und Konvektion ein noch größeres Gebiet erfassen kann.
Die sofortige Opferzahl lag in Hiroshima bei rund 70 000 Menschen und in Nagasaki bei etwa 40 000. Innerhalb eines Jahres stieg die Gesamtzahl der Opfer auf rund 140 000 in Hiroshima und 70 000 in Nagasaki. Viele Menschen starben zudem erst später an Verletzungen oder strahlenbedingten Krankheiten.
Radioaktivität
Zuerst einige Grundlagen zu Radioaktivität im Allgemeinen. Wenn wir sagen, ein Material habe eine Zerfallsrate von einem Zerfall pro Sekunde, bedeutet das, dass in jeder Sekunde ein Kern zerfällt. Dieser Zerfall kann über Alphastrahlung (Heliumkerne), Betastrahlung (Elektronen oder Positronen) oder Gammastrahlung (hochenergetische Photonen) erfolgen. Die Halbwertszeit gibt an, wie lange es dauert, bis die Hälfte der Kerne in einer Probe zerfallen ist.
Die Einheit für einen Zerfall pro Sekunde ist das Becquerel (Bq). (Weitere Einheiten sind Curie (Ci), mit $1 \text{ Ci} \approx 3,7 \times 10^{10} \text{ Bq}$, und Rutherford (Rd), wobei $1 \text{ Rd} = 10^6 \text{ Bq} = 1 \text{ MBq}$.) Diese Einheiten messen die radioaktive Aktivität, was für die Gesundheit an sich weniger aussagekräftig ist. Wesentlicher ist die Dosis bzw. Exposition – also die Energiemenge der Strahlung, die absorbiert wird, oder wie sie den Körper beeinflusst. Historisch wurden Einheiten wie Roentgen (R) und Gray (Gy) verwendet, doch für die Auswirkungen auf den menschlichen Körper ist heute der Sievert (Sv) am bedeutendsten, da hier unterschiedliche Strahlungsarten (alpha, beta, gamma) mit verschiedenen Bewertungsfaktoren berücksichtigt werden.
Typische Hintergrundstrahlung liegt bei etwa 2–3 Millisievert (mSv) pro Jahr. Gebiete gelten als kritisch, wenn sie mehr als einige Dutzend mSv pro Jahr erreichen. Bei akuter Strahlenbelastung können etwa 0,5–1 Sv schon sichtbare Strahlenkrankheiten hervorrufen, 2–5 Sv führen oft zu schweren Erkrankungen, und über 5 Sv sind für etwa die Hälfte der Betroffenen tödlich.
Unmittelbar nach dem Abwurf 1945 waren Personen in Bodennähe in Hiroshima akuten Dosen zwischen 1–6 Sv ausgesetzt. In den Folgemonaten kamen durch Fallout und Reststrahlung noch einmal etwa 0,5–1 Sv hinzu. In den darauffolgenden Jahren sank die Umweltdosis durch den Zerfall kurzlebiger Isotope schließlich auf nahe natürliche Werte von ungefähr 0,2–0,3 mSv pro Jahr. Heute liegt die Hintergrundstrahlung in diesen Städten, ähnlich wie in anderen Metropolen, bei etwa 1–2 mSv pro Jahr.
In Hiroshima waren etwa 5–15 % der Soforttodesfälle direkt auf die Strahlenkrankheit zurückzuführen, und in den Monaten nach dem Abwurf starben die meisten weiteren Opfer ebenfalls an strahlungsbedingten Erkrankungen. In Nagasaki zeigte sich ein ähnliches Bild.
Druckwelle und Feuersturm
Die Bomben wurden aus einer Höhe von etwa 9400 m abgeworfen, explodierten jedoch in rund 600 m über dem Boden, um die zerstörerische Wirkung zu maximieren. Von den etwa 20 Kilotonnen TNT-Äquivalent entfielen circa 40–50 % auf die Druckwelle, 30–50 % auf thermische Strahlung (extreme Hitze und Licht), etwa 5 % auf unmittelbare nukleare Strahlung und die restlichen 5–10 % auf Reststrahlung sowie die kinetische Energie von Bombensplittern.
Die Druckwelle breitete sich kugelförmig aus und zerstörte Gebäude in einem Umkreis von etwa 1500–2000 m um Ground Zero. Durch die extremen Temperaturen wurden in einem vergleichbaren Radius Brände ausgelöst, was zu einem Feuersturm führte, ähnlich wie bei den Brandbombenangriffen auf Tokio oder Dresden – die allerdings Tausende konventioneller Bomben erforderten anstelle einer einzigen. Insgesamt waren Druckwelle und Feuerball für rund 80–90 % der akuten Todesopfer in der unmittelbaren Umgebung verantwortlich.