Was ist es? Warum ist es interessant?
Betrachten wir ein einfaches Beispiel für ein Glücksspiel. Jemand bietet dir ein Spiel an, bei dem eine faire Münze geworfen wird: Du gewinnst 70 % des Geldes, das du gesetzt hast, wenn Kopf erscheint, und verlierst 60 % des Geldes, das du gesetzt hast, wenn Zahl erscheint. Außerdem hast du die Möglichkeit, dieses Spiel viele Male zu spielen, allerdings nicht beliebig oft, sagen wir einmal pro Tag. Intuitiv wirkt diese Wette vorteilhaft, besonders wenn man sie wiederholt spielen darf. Allerdings wird es komplizierter, wenn du dir Fragen stellst wie: „Wie viel meines gesamten Vermögens sollte ich setzen?“ und „Was ist die beste Strategie, um meinen langfristigen Wohlstand, sagen wir über 10 Jahre, zu maximieren?“ Das Kelly-Kriterium liefert die Antwort auf diese Fragen!
Um diese Fragen umfassend zu beantworten, brauchen wir ein paar Definitionen und Fachbegriffe (glaub mir, es zahlt sich aus).
Sei $a > 0$ der Prozentsatz deines Ausgangsvermögens, den du gewinnst, wenn Kopf erscheint, und sei $0 < b \leq 1$ der Anteil deines Ausgangsvermögens, den du verlierst, wenn Zahl erscheint. Sei außerdem $0 < p < 1$ die Wahrscheinlichkeit, dass Kopf erscheint (du gewinnst). Dann kann jede Wette wie folgt kategorisiert werden:
- Fair, wenn $a \cdot p = b \cdot (1 - p)$.
- Du hast einen Vorteil, wenn $a \cdot p > b \cdot (1 - p)$.
- Du hast einen Nachteil, wenn $a \cdot p < b \cdot (1 - p)$.
Als Nächstes definieren wir den Anteil $0 \leq f \leq \frac{1}{b}$ deines aktuellen Vermögens, den du setzen möchtest. (Bemerke: $\frac{1}{b}$ kommt daher, dass man immer sein ganzes Geld riskieren kann. Wenn nun $b < 1$, dann ist es auch möglich einen Hebel zu nehmen, solange im Verlustfall noch alles gedeckt ist.) Zur Vereinfachung der Notation gilt: Wenn du den Anteil $f$ deines Vermögens setzt: $$ a_f = a \cdot f, \quad b_f = b \cdot f.$$
Angenommen, du spielst dieses Spiel viele Male (möglicherweise beliebig oft). Dein Vermögen zum Zeitpunkt $t$ wird mit $X_t$ bezeichnet. Es kann definiert werden durch $$ X_{t+1} := X_t \cdot r_{t+1}, $$ wobei alle $$ r_t := \begin{cases} (1 + a_f),\text{ mit Wahrscheinlichkeit }p, \\ (1 - b_f),\text{ mit Wahrscheinlichkeit }(1-p) \end{cases} $$ unabhängig und identisch verteilt sind.
Eine entscheidende Frage ist:
$$ \text{Welches } f \text{ maximiert } X_t(f) \text{ nach vielen Spielen?}$$
Ein naiver Ansatz wäre, den Erwartungswert $E[X_t(f)]$ zu betrachten und $f$ so zu wählen, dass dieser Erwartungswert maximiert wird:
$$ \arg\max_{f} E[X_t(f)].$$
Um zu verdeutlichen, warum das problematisch sein kann, zeigen wir, dass das Maximieren des Erwartungswerts dazu führt, immer alles zu setzen, wenn wir einen Vorteil haben. Wenn du einen Anteil $f$ setzt, dann gilt:
- Mit Wahrscheinlichkeit $p$ ist dein neues Vermögen $X_0 \cdot (1 + a_f)$.
- Mit Wahrscheinlichkeit $1 - p$ ist dein neues Vermögen $X_0 \cdot (1 - b_f)$.
Das erwartete Vermögen nach einer Wette ist: $$ E[X_1] = p \cdot X_0 \cdot (1 + a_f) + (1 - p) \cdot X_0 \cdot (1 - b_f).$$
Faktorisiert man $X_0$ heraus, erhält man: $$ E[X_1] = X_0 \left[ p \cdot (1 + a_f) + (1 - p) \cdot (1 - b_f) \right].$$
Kombiniert man die Terme in den Klammern: $$ p \cdot (1 + a_f) + (1 - p) (1 - b_f) = p + p \cdot a_f + (1 - p) - (1 - p) \cdot b_f = 1 + f \bigl[p \cdot a - (1 - p) \cdot b\bigr].$$
Setzt man dies ein und erweitert diesen Ansatz auf ein beliebiges $t$, ergibt sich: $$ E[X_t] = X_0 \bigl[1 + f \cdot \bigl(p \cdot a - (1 - p) \cdot b\bigr)\bigr]^{t}.$$
Als Funktion von $f$ (im Intervall $0 \leq f \leq \frac{1}{b}$) ist dies ein monotoner Ausdruck.
Daraus folgt:
- Wenn $p \cdot a > b \cdot (1 - p)$ ist, dann ist der Koeffizient von $f$ positiv, und $E[X_1]$ wird maximiert, indem man $f = \frac{1}{b}$ wählt (d. h. alles setzt).
- Wenn $p \cdot a < b \cdot (1 - p)$ ist, ist der Koeffizient von $f$ negativ, sodass das Maximum bei $f = 0$ liegt (d. h. gar nicht setzen).
- Wenn $p \cdot a = b \cdot (1 - p)$, liefert jedes $f \in [0,\frac{1}{b}]$ das gleiche erwartete Vermögen.
Setzt man jedoch immer so viel möglich und riskiert sein ganzes Geld, wenn $p \cdot a > b \cdot (1 - p)$, dann kann man mit Sicherheit davon ausgehen, dass man nach wiederholtem Spiel bankrott geht. Dies ähnelt dem St. Petersburg-Paradoxon: Das Maximieren des Erwartungswertes einer wiederholten multiplikativen Wette kann zum Ruin führen.
Ein besserer Ansatz ist, die exponentielle Wachstumsrate deines Vermögens $X_t(f)$ zu optimieren. Formal suchen wir $$ \arg\max_{f} G(f),$$ wobei $$ G(f) := \lim_{t \to \infty} \frac{1}{t} \log \bigl(\frac{X_t(f)}{X_0}\bigr).$$
Angenommen, aus $t$ unabhängigen Versuchen sind $W$ Gewinne und $L$ Verluste (mit $W + L = t$). Jeder Gewinn multipliziert das aktuelle Vermögen mit $(1 + a_f)$, während jeder Verlust es mit $(1 - b_f)$ vervielfacht. Also gilt:
$$ X_t(f) = (1 + a_f)^W \cdot (1 - b_f)^L \cdot X_0.$$
Logarithmieren führt zu:
$$ G(f) = \lim_{t\to\infty} \Bigl[\frac{W}{t} \log \bigl(1 + a_f\bigr) + \frac{L}{t} \log \bigl(1 - b_f\bigr)\Bigr]$$
und unter Berücksichtigung, dass $W/t \to p$ und $L/t \to (1 - p)$ für $t \to \infty$, ergibt sich:
$$ G(f) = p \log \bigl(1 + a_f\bigr) + (1 - p) \log \bigl(1 - b_f\bigr).$$
Um den optimalen Anteil $f$ (den Kelly-Anteil) zu finden, setzt man die Ableitung von $G(f)$ nach $f$ gleich null und löst nach $f$ auf. Das Ergebnis lautet: $$ f_{\text{Kelly}} = \frac{p}{b} - \frac{1 - p}{a}.$$
Wenn du keinen Vorteil hast, d. h. wenn $$ p \cdot a \le b \cdot (1 - p),$$ dann ist $f_{\text{Kelly}} \le 0$, was bedeutet, dass du gar nicht wetten solltest. Umgekehrt liefert das Kelly-Kriterium bei einem Vorteil ($p \cdot a > b \cdot (1 - p)$) einen positiven Anteil zum Setzen—eine Balance zwischen dem Risiko des Ruins und dem potenziellen Wachstum, um deine Vermögenswachstumsrate langfristig zu maximieren.
Unten zeige ich eine Abbildung für die Parameter $ p=0.7, \text{ } a = 1.5, \text{ } b = 0.95 $. Beachte bitte, dass selbst in diesem vorteilhaften Spiel deine Wachstumsrate negativ werden kann, wenn du dein gesamtes Vermögen setzt!

Geschichte
Man könnte annehmen, dass Ideen wie das Kelly-Kriterium natürlicherweise im Kontext von Investitionen oder im Casino entstanden sind. Die ursprüngliche Herleitung kommt jedoch von einem etwas anderen Problem. 1956 entwickelte J. L. Kelly Jr., ein Forscher bei den Bell Labs (damals Teil von AT&T), das Kriterium, während er untersuchte, wie man Sportwetten optimiert, wobei man über einen rauschenden Kommunikationskanal Informationen zum Ausgang des zugrunde liegenden Ereignisses erhält—ein Konzept, das eng mit der Pionierarbeit der Forscher von Bell Labs in der Informationstheorie verbunden ist. Dieser Kontext ähnelt zwar der Ungewissheit in Aktienmärkten oder Casinospielen, aber die ursprüngliche Quelle des Zufalls in Kellys Arbeit stammte eher aus Signalrauschen als aus Marktereignissen oder Spielabläufen.
Claude Shannons Arbeit zur Informationstheorie führte zur Channel-Capacity als theoretische Grenze für fehlerfreie Kommunikation, ohne dabei das spezifische Kodierungsschema anzugeben. Kelly war der erste der es schaffte, die Verwendung der von Claude Shannon definierten Übertragungsrate ohne konkretes Kodierungsschema zu rechtfertigen und somit neu zu interpretieren. Um dieses Konzept zu veranschaulichen, entwickelte er ein Wettmodell, bei dem ein Spieler einen Informationsvorteil über einen rauschbehafteten Kommunikationskanal ausnutzen konnte. In diesem Kontext entdeckte Kelly im Wesentlichen Shannons Channel-Capacity neu, fasste sie jedoch als Entscheidungsfindung unter Unsicherheit auf. Genauere Details findest du in Kellys Originalarbeit „A New Interpretation of Information Rate“ aus dem Jahr 1956 (Link unten).
Ergodicity (-breaking)
Diesen Abschnitt kann man überspringen, ohne viel über das Kelly-Kriterium zu verpassen. Ich habe ihn trotzdem aufgenommen, weil ich denke, dass Ergodicity, obwohl nicht direkt mit dem Kelly-Kriterium verbunden, eng damit verwandt und sogar eine Verallgemeinerung des Phänomens ist, bei dem sich arithmetische Eigenschaften eines Zufallsprozesses von den geometrischen unterscheiden. Insbesondere beleuchtet sie den Ergodicity den Unterschied zwischen einem Ensemble und einer einzigen Realisierung eines Prozesses.
Informell nennt man einen Zufallsprozess $ X_t $ ergodic, wenn dessen Zeit-Mittelwert einer beliebigen wohldefinierten Funktion dem entsprechenden Ensemble-Mittelwert (Erwartungswert) entspricht. In diskreter Zeit sieht man das wie folgt:
$$ \lim_{T \to \infty} \frac{1}{T} \sum_{t=1}^{T} f\bigl(X_t\bigr) = \mathbb{E}\bigl[f(X_t)\bigr], $$
für jede integrierbare Funktion $f$. Äquivalent bedeutet das, dass der „Zeit-Mittelwert“ entlang eines unendlich langen Pfades gegen den „Ensemble-Mittelwert“ über alle möglichen Pfade konvergiert.
Ein non-ergodic Prozess ist ein Prozess, bei dem mindestens eine Funktion $f$ die Gleichheit von oben nicht einhält—d. h. bei dem sich Zeit-Mittelwert und Ensemble-Mittelwert nicht decken.
Als Nächstes betrachten wir ein einfaches Beispiel für einen ergodic Prozess: Den einfachen Münzwurf. In jedem diskreten Schritt $ t $ werfen wir eine Münze, die mit $ 60 $ % Kopf und $ 40 $ % Zahl landet. Zeigt die Münze Kopf, gewinnst du $ +1 $, bei Zahl verlierst du $ -1 $. Das bedeutet, du hast einen positiven arithmetischen Vorteil. Also gilt $ X_t \in \{ +1, -1 \} $ mit den Wahrscheinlichkeiten $ 0.6 $ bzw. $ 0.4 $. Der Ensemblemittelwert eines Wurfs ist $ 0.2 $. Der Zeit-Mittelwert einer langen Sequenz konvergiert nach dem Gesetz der großen Zahlen ebenfalls zu $ 0.2 $, was die Ergodicity zeigt. Unten siehst du eine Simulation dieses Münzwurfprozesses:
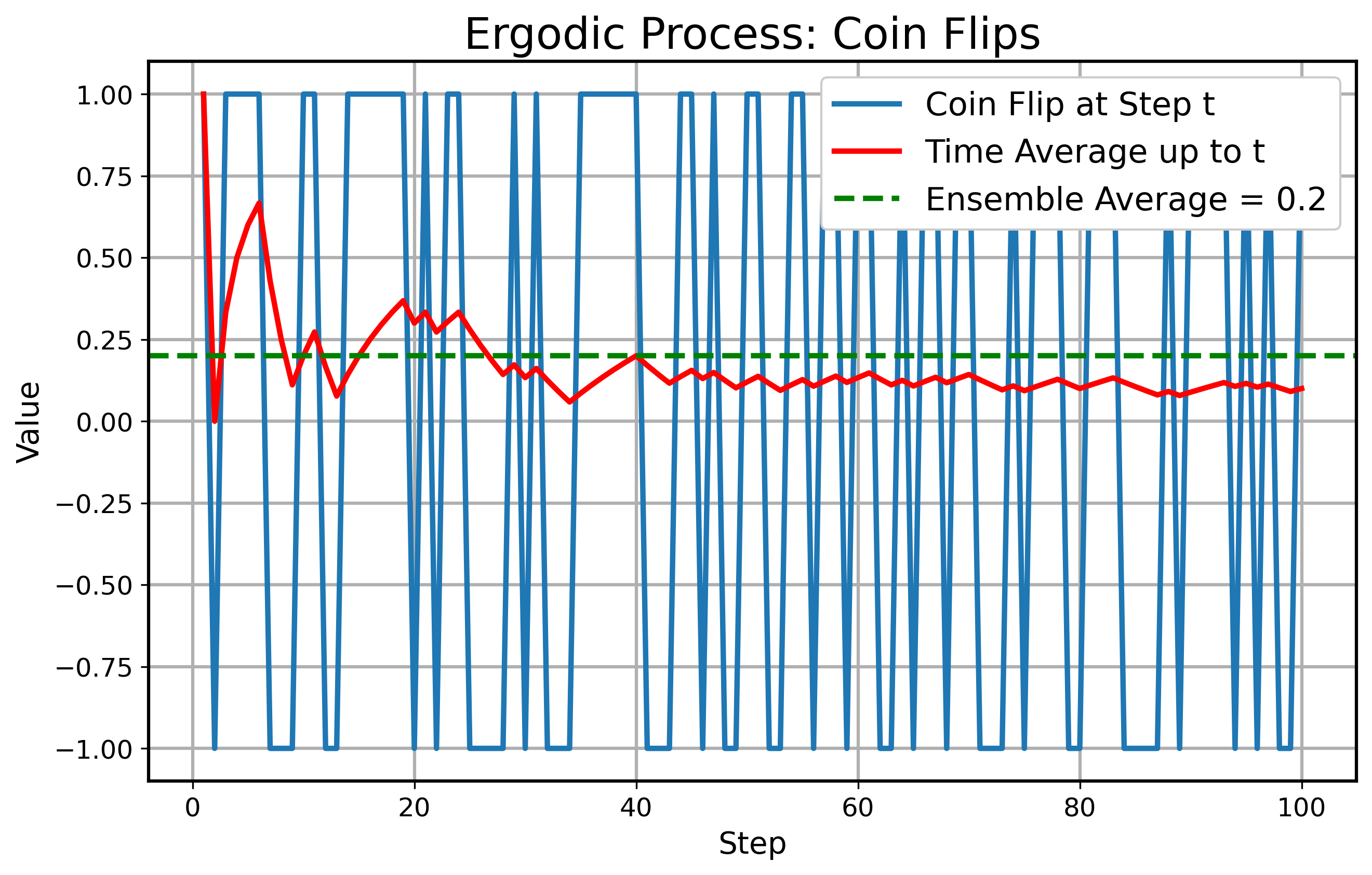
Für ein Beispiel eines non-ergodic Prozesses betrachten wir multiplikatives Wachstum. Ein Vermögen zum Zeitpunkt $ t $, bezeichnet als $ X_t $, entwickelt sich multiplikativ:
$$ X_{t+1} = X_t \cdot r_{t+1},$$
wobei $ r_{t+1} $ ein Zufallsfaktor ist. In diesem Beispiel sei: $ r_{t+1} \in \{ 1.7, 0.5 \}$ mit Wahrscheinlichkeit $ 0.5 $ jeweils, und $ X_0 = 1 $. Der Ensembledurschnitt bei Zeitpunkt $ t $:
$$ E[Y_t] = \left(0.5 \cdot 1.7 + 0.5 \cdot 0.5\right)^t = 1.1^t.$$
Da der geometrische Mittelwert aber unter $ 1 $ liegt,
$$ \exp(0.5 \cdot \log(1.7) + 0.5 \cdot \log(0.5)) = 0.92,$$
driftet der Einzelpfad häufig langfristig unter 1. Obwohl das Ensemblemittel mit $ 1.1^t $ wächst, liegen die meisten Einzelrealisierungen langfristig unter 1. Daraus folgt:
$$ \text{Zeit-Mittelwert} \neq \text{Ensemble-Mittelwert} \rightarrow \text{non-ergodic}.$$
Unten siehst du eine Simulation dieses Prozesses:

Dieses Beispiel verdeutlicht, was auch in unserem anfänglichen Beispiel passiert ist. Obwohl der Vorteil offensichtlich positiv ist (was im grünen, gestrichelten Ensemblemittelwert sichtbar wird), wird der Einzelpfad in einem multiplikativen Prozess meist negativ.
Kelly als mögliche Lösung für non-ergodic multiplikatives Wachstum
Das „Ergodicity Problem“ bezieht sich auf Fälle, in denen Forschende irrtümlich Ensemblemittelwerte auf Systeme anwenden, bei denen der Zeit-Mittelwert die relevante Größe ist. Dies führt oft zu irreführenden Schlussfolgerungen, besonders in Systemen, in denen sich Zeit-Mittelwert und Ensemble-Mittelwert nicht decken. Das Problem kann auch umgekehrt auftreten—wenn Forschende sich auf Zeit-Mittelwerts konzentrieren, obwohl Ensemblemittelwerte passender wären oder die Zeit-Mittelwerts nicht existieren. In non-ergodic Systemen kann sich der Zeit-Mittelwert zwischen einzelnen Realisierungen eines Zufallsprozesses stark unterscheiden.
Im konkreten Fall von Prozessen mit multiplikativem Wachstum bietet das Kelly-Kriterium eine Lösung für das Ergodicity Problem. Das Kelly-Kriterium maximiert die langfristige, multiplikative Wachstumsrate des Vermögens, indem es den geometrischen Mittelwert der Renditen optimiert. Mathematisch entspricht dies der Maximierung des Zeit-Mittelwerts eines multiplikativen Wachstumsprozesses, wie unten gezeigt wird. Darüber hinaus lässt sich zeigen, dass die Wachstumsrate (oder eine beliebige wohldefinierte Wachstumsrate) ein Beispiel für eine ergodic Observable ist—eine, bei der der Zeit-Mittelwert mit dem Ensemble-Mittelwert übereinstimmt.
Mehr über das Ergodicity Problem und ergodic Observables findest du in den Blogbeiträgen und wissenschaftlichen Arbeiten von Ole Peters (Link unten).
Investieren
Das Kelly-Kriterium und seine Varianten treten natürlich auch beim Investieren auf. Da es beim Investieren um multiplikatives Wachstum geht und jeder Mensch nur ein Leben hat, um die „Würfel zu werfen“, ist es entscheidend, die Zufälligkeit so gut wie möglich zu kontrollieren—insbesondere wenn die Chancen günstig stehen.
Safe-Haven-Investing
Ein Buch, das Ideen über multiplikatives Wachstum, Ergodicity, das Kelly-Kriterium und Versicherungsstrategien im Investieren zusammenbringt, ist Safe Haven von Mark Spitznagel. Da dieses Buch eine große Inspiration für diesen Blogbeitrag war, empfehle ich es jedem, der sich für diese Themen interessiert (Link unten).
In diesem Beitrag gehe ich nicht auf den Hauptfokus des Buches ein—nämlich wie Investitionen mit einer Art „Versicherungskomponente“ zu einer höheren multiplikativen Wachstumsrate, als das Kelly-Kriterium führen können. Stattdessen möchte ich einige subtile Punkte aus dem Buch hervorheben, die mehr Aufmerksamkeit verdienen. Zuvor erinnere ich noch and die Definition des geometrischen Mittelwerts und des Medians von diskreten beziehungsweise stetigen Verteilungen, weil diese benötigt werden:
Geometrisches Mittel $ GM $:
$$ GM = \exp \left( \sum_{i} p(x_i) \cdot \log (x_i) \right), \quad GM = \exp \left( \int_{0}^{\infty} \log (x) \cdot p(x) dx \right).$$
Median $ m $:
$$ \sum_{x_i \leq m} p(x_i) = \frac{1}{2}, \quad \int_{0}^{m} p(x) dx = \frac{1}{2}.$$
Nun zu den interessanten Aussagen:
Die Optimierung der multiplikativen Wachstumsrate ist gleichbedeutend mit der Optimierung des geometrischen Mittels der Schlussverteilung des Prozesses und damit äquivalent zur Optimierung der erwarteten logarithmischen Utility des Prozesses.
Die Optimierung des geometrischen Mittels der Schlussverteilung ist mathematisch gleichbedeutend mit der Optimierung der Median der Schlussverteilung.
Um andere Perzentile zu optimieren, etwa das 5. Perzentil ($q_{0.05}$), kann man das fractional Kelly Criterion verwenden. Dabei setzt man einen Faktor $\alpha$ des vollen Kelly-Anteils, mit $\alpha < 1$. Beispielsweise erhält man bei $\alpha = \frac{1}{4}$ einen Wettanteil:
$$ f = \frac{1}{4} \cdot f_{\text{Kelly}}.$$
Diese Strategie balanciert Wachstum und Risiko aus und ermöglicht es, bestimmte Perzentile der Vermögensverteilung gezielt zu optimieren.
Im nächsten Abschnitt werde ich diese Punkte präzisieren und zeigen, dass sie zwar (wie im Buch beschrieben) stimmen, jedoch nicht alle gleichzeitig völlig korrekt sein können. Konkret:
- Punkt (1) ist immer gültig.
- Punkt (2) trifft nur zu, wenn $t$ gegen unendlich geht.
- Punkt (3) gilt, wenn $t$ endlich ist, und der exakte Anteil von Kelly, der ein bestimmtes Perzentil maximiert, hängt von $t$ ab.
Dies bedeutet, dass (2) und (3) sich etwas widersprechen.
Unterschied zwischen endlichem und unendlichem Fall
In den folgenden Abschnitten betrachten wir den Prozess des multiplikativen Wachstums $ X_t $ und verwenden die gleiche Notation wie zuvor.
Äquivalenzen
Um Verwirrung zu vermeiden beachte, dass die Maximierung der exponentiellen Wachstumsrate
$$ G(f) = \lim_{t \to \infty} \frac{1}{t} \log \bigl(\frac{X_t(f)}{X_0}\bigr) $$
hinsichtlich $ f $ äquivalent ist zu
- der Maximierung der erwarteten logarithmischen Utility $$ \arg\max_{f} \bigl(E[\log (X_t(f))]\bigr) $$ (wie von Bernoulli vorgeschlagen, um das St. Petersburg-Paradoxon zu lösen), und
- der Maximierung des geometrischen Mittels der Verteilung zum Zeitpunkt $ t $, $$ \arg\max_{f} (GM).$$
Letztlich steckt in allen Ausdrücken $$ \log (X_t(f)) $$ und nur das geometrische Mittel ist in die monotone Exponentialfunktion verpackt, was das $\arg\max$ nicht verändert.
Unendlicher Fall
Hier betrachten wir den Grenzfall $ t \to \infty $. Es ist hilfreich, die Grenzverteilung des Prozesses zu untersuchen, wenn $ t $ groß wird. Da es sich um einen multiplikativen Prozess handelt und die Zufallsfaktoren $ \text{u.i.v.} $ sind, nähert sich die Verteilung einer Lognormalverteilung gemäß dem Zentralen Grenzwertsatz. Konkret betrachten wir $ \log (X_t) $ (ich gebe die explizite Abhängigkeit von $ f $ bewusst an):
$$ \log (X_t) = \log (X_0) + \sum_{n=1}^t \log \bigl(r_t(f)\bigr). $$
Nun definieren wir die Zufallsvariable $ Y_t $:
$$ Y_t := \log \bigl(r_t(f)\bigr), $$
die einen Erwartungswert und eine Varianz hat:
$$ \mu(f) = E \bigl[ Y_t \bigr], \quad \sigma^2(f) = \mathrm{Var}\bigl(Y_t\bigr). $$
Nach dem Zentralen Grenzwertsatz ist die Summe $ \sum_{n=1}^t Y_t $ normalverteilt mit den Parametern
$$ t \cdot \mu(f), \quad t \cdot \sigma^2(f). $$
Daher ist $ X_t $ lognormalverteilt mit den Parametern
$$ \log (X_0) + t \cdot \mu(f), \quad t \cdot \sigma^2(f). $$
Als Nächstes betrachten wir, welche Anteile $ f $ bestimmte Perzentile der lognormalen Verteilung optimieren. Man kann die Normalverteilung von $ \sum_{n=1}^t Y_t $ wie folgt schreiben:
$$ \sum_{n=1}^t Y_t \sim t \cdot \mu (f) + \sqrt{t} \cdot \sigma (f) Z, $$
wobei $ Z \sim N(0,1) $ eine Standardnormalverteilung ist.
Betrachten wir ein bestimmtes Perzentil $q \in (0,1)$—etwa das 10. Perzentil, den Median (50.) oder das 90. Perzentil—der Verteilung von $ X_t $. Wir bezeichnen dieses Perzentil mit $Q_q(X_t)$. Formal ist $Q_q(X_t)$ diejenige Zahl $x$, für die
$$ P\bigl(X_t \le x\bigr) = q. $$
Entsprechend im Logarithmischen:
$$ Q_q\bigl(\log (X_t)\bigr) = \log \Bigl(Q_q(X_t)\Bigr). $$
Verwendet man die approximative Normalverteilung aus dem Zentralen Grenzwertsatz (für großes $t$, Annahme u.i.v.):
$$ \log X_t \approx \log X_0 + t \cdot \mu(f) + \sqrt{t} \cdot \sigma(f) Z. $$
Für eine Standardnormalverteilung $Z$ ist das $q$-Perzentil eine Konstante $z_q$ (z. B. $z_{0.5} = 0$ für den Median). Also gilt:
$$ Q_q\bigl(\log X_t\bigr) \approx \log X_0 + t \cdot \mu(f) + \sqrt{t} \cdot \sigma(f) , z_q. $$
Durch Exponenzieren erhält man:
$$ Q_q(X_t) = \exp \Bigl(Q_q(\log X_t)\Bigr) \approx X_0 \exp \Bigl(t \cdot \mu(f) + \sqrt{t} \cdot \sigma(f) , z_q\Bigr). $$
Wir suchen
$$ \arg \max_f \Bigl( t \cdot \mu(f) + \sqrt{t} \cdot \sigma(f) , z_q \Bigr). $$
Leitet man nach $f$ ab und setzt gleich null:
$$ \frac{d}{df}\Bigl[ t \cdot \mu(f) + \sqrt{t} \cdot \sigma(f) , z_q\Bigr] = t \cdot \mu’(f) + \sqrt{t} \cdot z_q , \sigma’(f) = 0. $$
Daraus folgt:
$$ \mu’(f) + \frac{z_q}{\sqrt{t}} \sigma’(f) = 0. $$
Im Grenzwert $t \to \infty$ gilt:
$$ \frac{z_q}{\sqrt{t}} \to 0. $$
Daher verschwindet der Term mit $\sigma’(f)$, und es bleibt $ \mu’(f) = 0 $, was genau folgendem entspricht:
$$ \arg\max_{f} \bigl(E [ \log (X_t(f)) ]\bigr). $$
Das heißt, der optimale Wert $f$ für jedes festgelegte Perzentil $q$ konvergiert gegen den gleichen Wert $f_{\text{Kelly}}$, der $\mu(f)$ maximiert, also der erwarteten logarithmischen Utility und damit $G(f)$, die exponentielle Wachstumsrate. Mit anderen Worten wird der Kelly-Anteil für alle Perzentile optimal, sobald $t \to \infty$.
Diese Herleitung ist sehr mühsam, deswegen möchte ich sicher gehen, dass du die Intuition verstehst. Solange $f$ steigt und noch unter dem optimalen Anteil $ f_{\text{Kelly}} $ liegt, nehmen sowohl die Wachstumsrate als auch die Varianz der Verteilung zu. Geht man jedoch über den Kelly-Anteil hinaus, wird es gefährlich: Die Wachstumsrate sinkt wieder, während die Varianz weiter zunimmt! Daher empfehlen Praktiker oft, etwas unterhalb des optimalen Anteils zu bleiben. Im endlichen Setting (wie im nächsten Abschnitt) kann dies dazu führen, dass man für tiefere Perzentile mit einer fractionalen Kelly-Strategie unter dem optimalen Anteil bleibt und für höhere Perzentile ggf. über diesem Anteil. Im Grenzfall $ t \to \infty $ überwiegt jedoch die optimale Wachstumsrate den Einfluss niedriger/höherer Varianzen, sodass dieser Anteil für alle Perzentile optimal wird!
Endlicher Fall
Nun betrachten wir den Fall, dass $ t $ endlich bleibt. Da eine analytische Analyse von $ X_t $ für beliebiges endliches $ t $ eine sehr aufwendige Herleitung der Verteilung von $ X_t $ erfordern würde, die von $ r_t $ abhängt, verwenden wir hier Simulationen, um zu veranschaulichen, was passiert. Darüber hinaus ist für fast jede Verteilung von $ r_t $ und jedes endliche $ t $ die Verteilung von $ X_t $ nicht exakt lognormal; nur in diesem (oder anderen speziellen Fällen) Fall würde der Median von $ X_t $ mit dem geometrischen Mittel übereinstimmen.
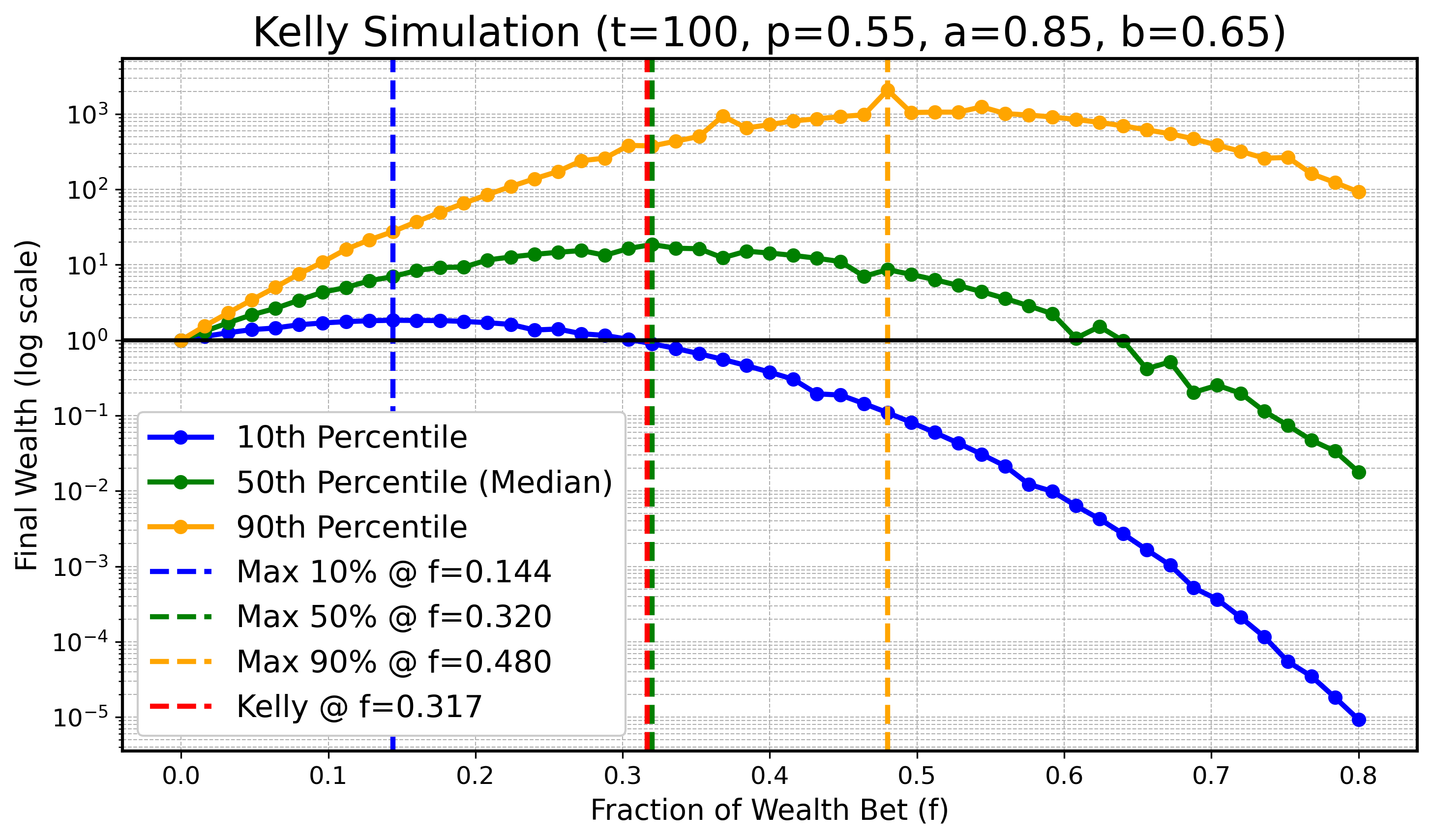
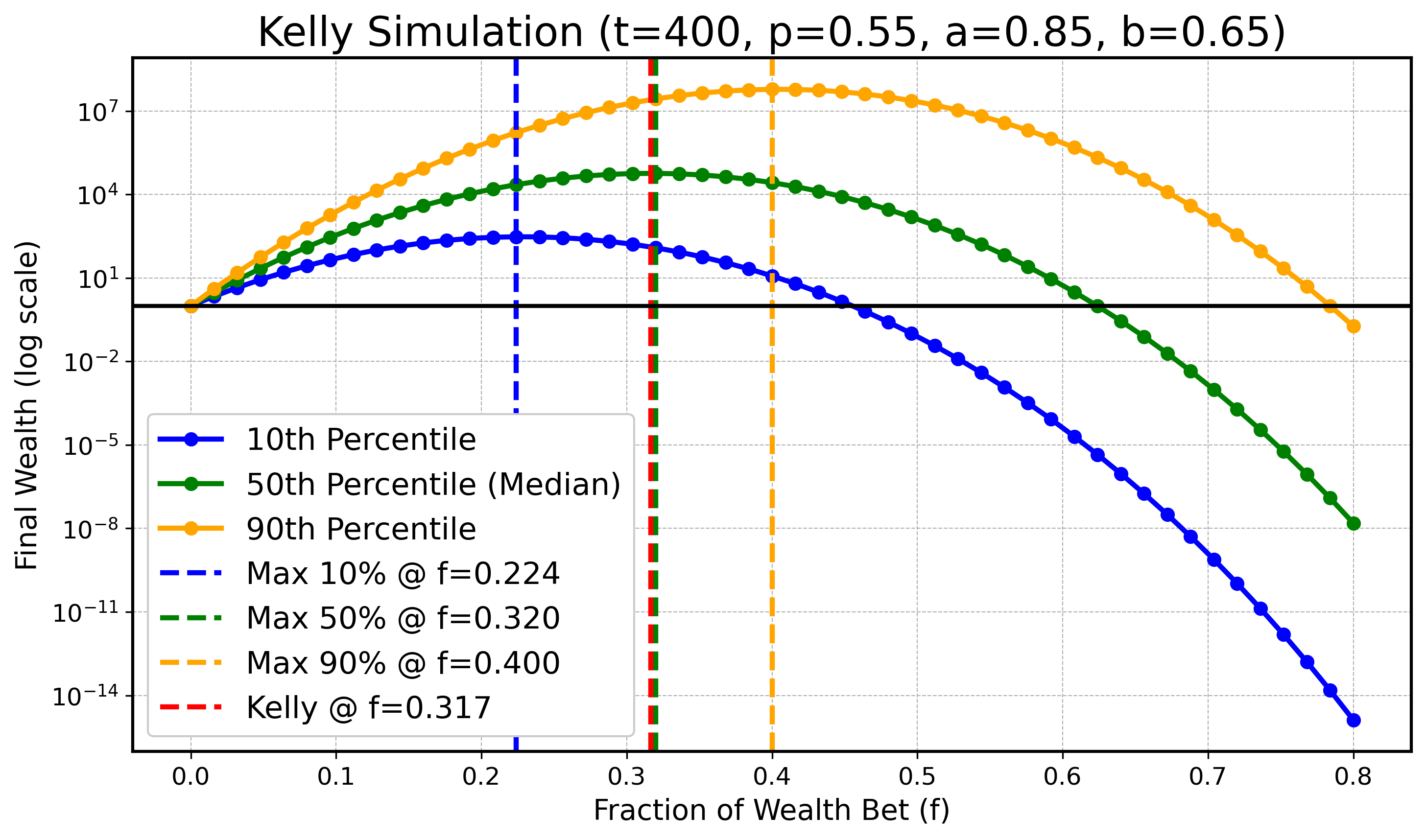
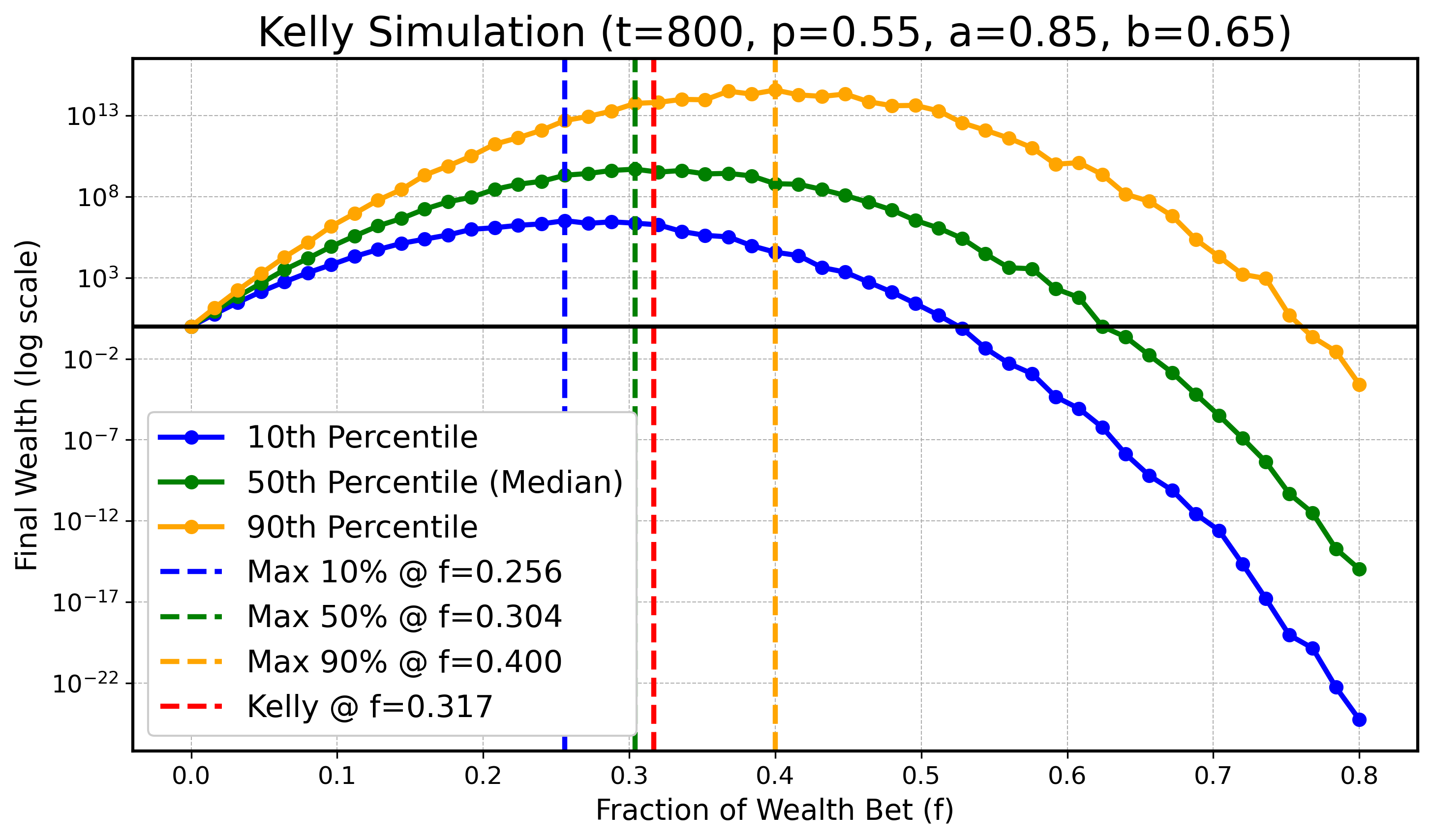
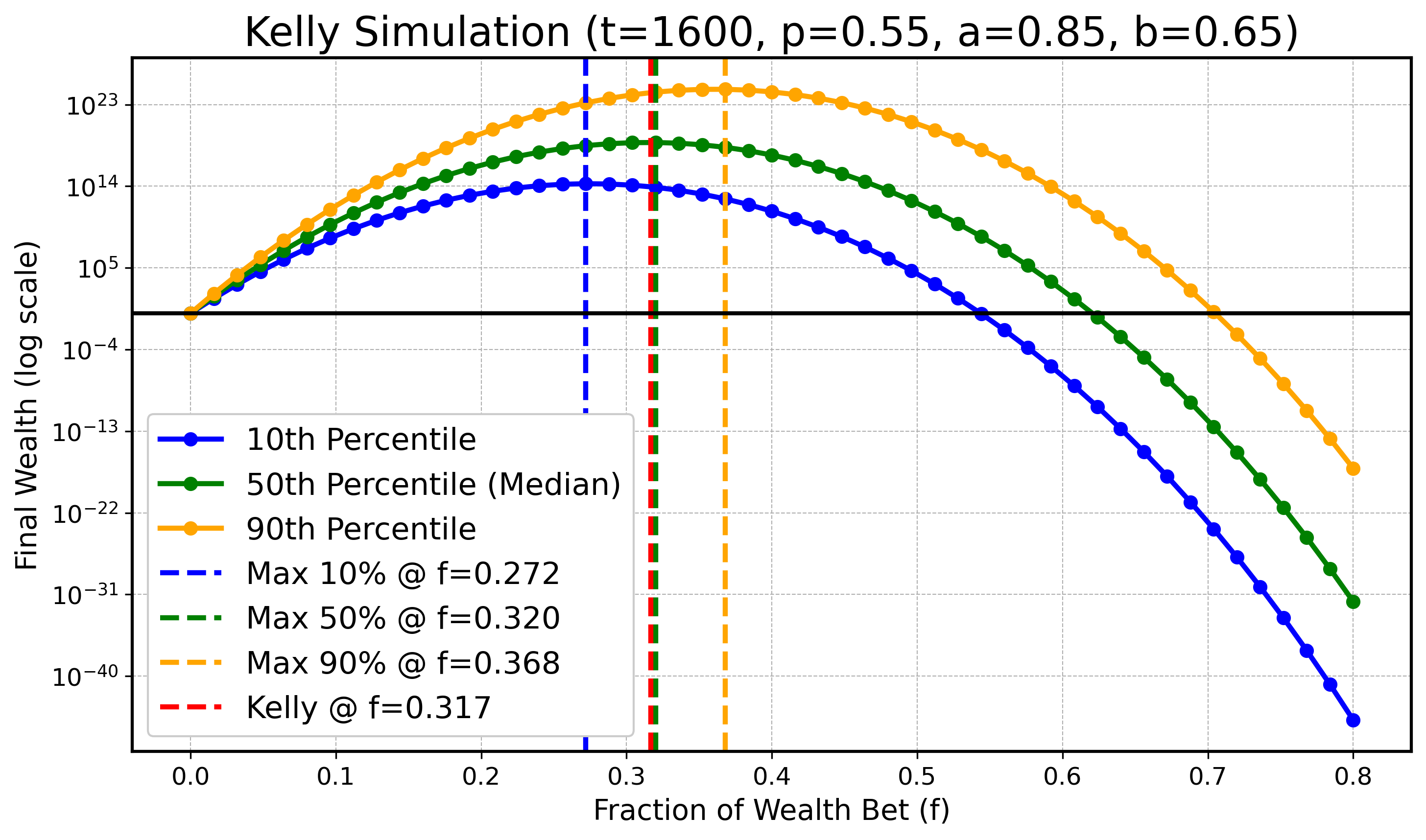
Wir werden eine Simulation durchführen, um zu illustrieren, dass bei endlichem $ t $ das Optimum für tiefere oder höhere Perzentile kleiner bzw. größer als $ f_{\text{Kelly}} $ sein kann, während sich diese optimalen Werte für die Perzentile mit wachsendem $ t $ an $ f_{\text{Kelly}} $ annähern. Konkret betrachten wir $ X_t $ wie zuvor mit den Parametern:
$$ a=0.9, \text{ } b=0.6, \text{ } p=0.55, $$
und $ t \in \{ 100, 200, 400, 800, 1600, 3200 \} $. In allen folgenden Diagrammen zeichnen wir den optimalen Kelly-Anteil in Rot ($ f_{\text{Kelly}} $) und die optimalen Anteile für $ q_{0.1} $ (blau), den Median $ q_{0.5} $ (grün) sowie $ q_{0.9} $ (orange) als gestrichelte Vertikallinien ein.
$t = 100$:
$t = 200$:

$t = 400$:
$t = 800$:
$t = 1600$:
$t = 3200$:
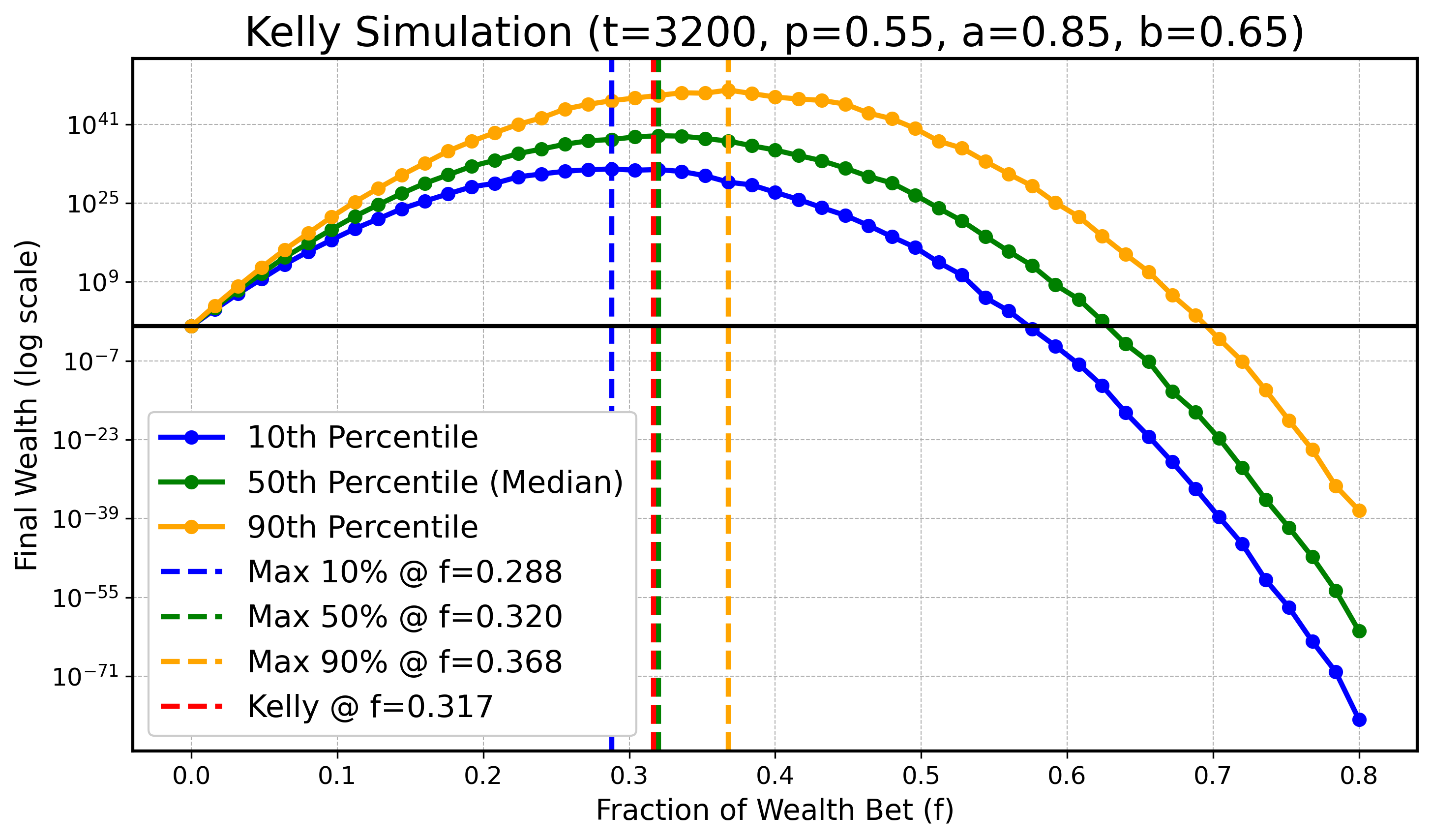
Obwohl es leichte numerische Ungenauigkeiten wegen begrenzter Simulationsressourcen gibt, erkennt man klar den Trend: Mit steigendem $ t $ rücken die optimalen Anteile für das 10. und das 90. Perzentil näher an den optimalen Median-Anteil und damit an den theoretisch optimalen Anteil $ f_{\text{Kelly}} $ heran.
Fazit
Ziel dieses Blogbeitrags war es, das Kelly-Kriterium so intuitiv wie möglich und so genau wie nötig zu erklären. Zwar ist die Herleitung und Erklärung des Kelly-Kriteriums selbst nicht einzigartig und kann auf vielen anderen Seiten gefunden werden, jedoch empfehle ich, das Originalpaper zu lesen, um die historischen und kontextuellen Hintergründe zu verstehen.
Zusätzlich zur Einführung des Kriteriums wollte ich es in den größeren Kontext der Ergodicity stellen—ein interessantes Thema, das ein tieferes Verständnis des Kelly-Kriteriums und seiner praktischen Anwendungen ermöglicht.
Die Hauptmotivation für diesen Beitrag ergibt sich jedoch aus den subtilen und zum Nachdenken anregenden Argumenten in Mark Spitznagels Safe Haven. Mein Ziel war es, die subtilen Unterschiede zwischen den unendlichen und endlichen Fällen des Kelly-Kriteriums zu verdeutlichen, die oft schwer zu verstehen sind und online selten klar erklärt werden. Ich hoffe, dass meine Ausführungen helfen, diese Konzepte zu erhellen und einige Missverständnisse aufzulösen.
Wichtige Erkenntnisse:
Vereinheitlichte Optimierung Die Optimierung der exponentiellen Wachstumsrate $G(f)$, der erwarteten logarithmischen Utility $ \mathbb{E} \big[ \log(X_t(f)) \big] $ und des geometrischen Mittels $ \text{GM}(X_t(f)) $ führt stets zum gleichen Maximierer: $ f_{\text{Kelly}} $.
Median vs. Geometrisches Mittel Der Median der Vermögensverteilung $ X_t $ fällt nur im unendlichen Fall mit ihrem geometrischen Mittel zusammen, wenn der Zentrale Grenzwertsatz die Verteilung in Richtung einer Lognormalverteilung bringt.
Endliche vs. Unendliche Horizonte Dies ist der entscheidendste Punkt: Eine fractionale Kelly-Strategie (d. h. ein Teil von $ f_{\text{Kelly}} $) optimiert nur ein niedrigeres Perzentil der Vermögensverteilung bei einem endlichen Zeithorizont $t$. Da wir als Menschen alle endlich leben, ist das möglicherweise durchaus sinnvoll. Allerdings hängt der optimale Anteil von $ f_{\text{Kelly}} $ stark von $t$ ab.
- Wenn $ t \to \infty $, konvergiert dieser Anteil gegen 1, das heißt, $ f_{\text{Kelly}} $ wird für alle Perzentile optimal.
- Das ist eine gute Nachricht für alle Spieler und Investoren: Je länger du das Spiel spielst, desto weniger spielt es eine Rolle, welches Perzentil du optimieren willst.
- Dennoch ist es wichtig anzumerken, dass ein geringerer Einsatz als $ f_{\text{Kelly}} $ in endlichen Fällen oft bessere Ergebnisse bringen kann, da er die Varianz der Verteilung des Vermögens reduziert.
Ich hoffe, dieser Beitrag bietet sowohl Klarheit als auch praktische Einblicke in das Kelly-Kriterium, seine Anwendungen und seine Implikationen für Entscheidungsprozesse in endlichen und unendlichen Horizonten.